LeetCode：螺旋矩阵 II

题目

给你一个正整数 n ，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

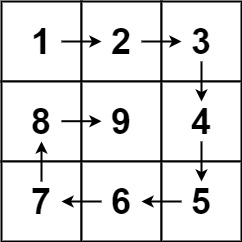
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 20

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/spiral-matrix-ii

思路

如图我们定义左上角的坐标为 0,0，横轴为 x 轴；竖轴为 y 轴。

即 matrix[1] 的下标为 y-1；值分别为 {y-1,x-1}...

而我们要控制的就是起始点 1,1 开始按 右下左上 的循环逻辑去移动即可，并且保证点在合理的区域内。

代码

Go

package main

import "fmt"

// 点位置
type point struct {
	x int
	y int
}

func generateMatrix(n int) [][]int {
	matrix := make([][]int, n)

	// 初始值
	for i := 0; i < n; i++ {
		matrix[i] = make([]int, n)
	}

	p := point{1, 1} // 初始位置，坐标(左上角)
	dir := "r"       // 默认方向
	p_max := n
	p_min := 1

	for i := 1; i <= n*n; i++ {
		fmt.Println(p)
		matrix[p.y-1][p.x-1] = i

		switch dir {
		case "r":
			p.x += 1
			break
		case "d":
			p.y += 1
			break
		case "l":
			p.x -= 1
			break
		case "t":
			p.y -= 1
			break
		}

		// 下一步的方向
		if dir == "r" && p.x == p_max {
			dir = "d"
		}
		if dir == "d" && p.y == p_max {
			dir = "l"
			p_max -= 1
		}
		if dir == "l" && p.x == p_min {
			dir = "t"
			p_min += 1
		}
		if dir == "t" && p.y == p_min {
			dir = "r"
		}
	}

	return matrix
}

func main() {
	fmt.Println(generateMatrix(2))
	fmt.Println(generateMatrix(3))
	fmt.Println(generateMatrix(4))
}